Kapitola 3: Operace s binárními čísly v mikroprocesoru
3.1 Úvod
V počítači se aritmetické operace provádějí v 8 bitech, 16 bitech, 32 bitech nebo 64 bitech. Číslo jako 3 v binárním systému je 11. Pokud má být operace provedena v 8 bitech, považuje se to za 00000011; před ním s 0 nulami.
Pro binární číslo, jako je 10000101, je nejvýznamnější bit bit zcela vlevo. V tomto případě je 1. Nejméně významný bit je krajní bit vpravo, který je stále 1 pro číslo. Nejvýznamnější bit je zkrácen jako MSB. Nejméně významný bit se označuje zkratkou LSB.
BInary digiT je zkráceno jako BIT a je jednoduše psáno jako bit. V čísle 10010011 je každá jednička nebo nula bit. Skupina čtyř bitů se nazývá nibble. Skupina osmi bitů se nazývá byte. Byte se skládá ze dvou kousků. Nižší okus je okus pro LSB a vyšší okus je okus pro MSB.
Skupina 8 bitů, 16 bitů, 32 bitů nebo 64 bitů se nazývá slovo, pokud tato skupina přenáší informace nad rámec pouhého označení čísla. Skupina se nazývá slovo, například pokud se jedná o nízkoúrovňovou instrukci v počítači. Existuje také slovo 24 bitů, ale to se dnes běžně nepoužívá.
Endianness odkazuje na pořadí, ve kterém bajty tvoří slovo. Zvažte 24bitové slovo – 100100001111010100100010. Toto slovo se skládá ze tří bajtů, které jsou:
10010000 11110101 00100010
Nejvýznamnější bajt je bajt nejvíce vlevo. Když je bajt na krajní levé straně nejvýznamnější bajt a bajt na krajní pravé straně je nejméně významný bajt, označuje se to jako reprezentace slova Big Endian. Reprezentace Little Endian je opakem.
Paměť počítače je řada buněk a každá buňka obsahuje bajt. První buňka v paměti počítače je pro bajt 0, druhá je pro bajt 1, třetí je pro bajt 2 a tak dále. Při velké endianness a pro předchozí slovo je nejvýznamnější bajt uložen v buňce bajtu 0, prostřední bajt je uložen v buňce 1 a nejméně významný bajt je uložen v buňce 2. To znamená, že ve spodní paměťové buňce je více významných bajtů.
Předchozí 24bitové slovo lze zapsat v obráceném pořadí bajtů takto:
00100010 11110101 10010000
Nyní je nejméně významný bajt zcela vlevo a nejvýznamnější bajt je zcela vpravo. Když je bajt zcela vlevo nejméně významný bajt a bajt zcela vpravo je nejvýznamnější bajt, jedná se o reprezentaci slova Little Endian. S malou endianness a pro předchozí slovo je nejméně významný bajt uložen v buňce bajtu 0, prostřední bajt je uložen v buňce 1 a nejvýznamnější bajt je uložen v buňce 2. To znamená, že v dolní paměťové buňce je méně významný bajt.
Endianness se nepoužívá pro bity v bajtu. Také se nepoužívá pro kousání v byte. Používá se pouze pro pořadí bajtů.
Číselná řada
Číslo bez znaménka je kladné číslo. Kladná čísla jsou čísla od nuly nahoru. Existují i záporná čísla. Na číselné ose mohou být uvedena kladná a záporná čísla. Následující číselná řada ukazuje kladná a záporná celá čísla (celá čísla) blízko nuly:
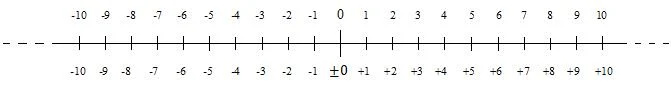
Záporná čísla klesají od nuly dolů (doleva). V mnoha situacích je nula považována za kladnou. V některých situacích je však považován za negativní. Proto je v diagramu před nulou v nižším číslování znaménko plus a mínus. Když je číslo kladné, jeho znaménko lze vynechat; to je případ horního číslování v diagramu. Znaménko mínus před záporným číslem se nikdy nevynechává.
3.2 Sčítání binárních čísel
Kromě toho:
A + B = S
A se nazývá augend, B se nazývá sčítanec a S se nazývá součet.
Zvažte následující sčítání dvou kladných čísel v základu dva:

V základu dva jsou jediné možné číslice 0 a 1. Sčítání v základu 2 je podobné sčítání v základu deset, ale dvojka v základu dva je jedna nula (10). Když je součet dvou bitů ve sloupci 10, zapíše se 0 a 1 se přenese do bezprostředního levého sloupce; se přičte k součtu tamních dvou bitů. Když je celkový součet tři, znamená to 11 v základu dva. Pravá 1 v 11 se zapíše a levá 1 se přenese, aby se přidala k součtu bitů bezprostředního levého sloupce. V obou případech se 1 nesená doleva nazývá nesení.
Při čtení předchozí tabulky sčítání zprava je ve druhém sloupci (zprava) přenos, který je výsledkem 1+1 = 10. Ve třetím sloupci je přenos, který je výsledkem 1+1+ přenos 1 = 11. Ve čtvrtém sloupci je přenos, který je výsledkem 0+1+ přenosu 1 = 10. V pátém sloupci není přenos, protože součet je 0+0+ přenos 1 = 1. zbytek sloupců nezahrnuje žádné přenášení.
Počítání sloupců začíná od pravého konce. S 16bitovým sčítáním může dojít k přenosu z osmého sloupce do devátého sloupce (pohyb doleva). Ilustruje to následující tabulka:

Aritmetické a logické operace probíhají v mikroprocesoru na základní desce počítače.
U 8bitového wordového počítače nemůže přenos přejít z osmého bitu na devátý bit automaticky pomocí hardwaru. Chcete-li tedy v takovém počítači přidat dvě 16bitové skupiny, musí být přidání provedeno dvakrát v osmi-osmibitových párech. Přenos se pohybuje a provádí pomocí softwaru (programování).
Chcete-li přidat dvě čísla, lze čísla před přidáním nejprve převést na formu doplňku jejich dvojky (viz níže).
3.3 Doplnění dvojky a její odečítání binárních čísel
Na základní desce počítače je paměť a tam je mikroprocesor a další obvody. Paměť je série osmibitových buněk. U bajtu jde každý bit do buňky. Mikroprocesor má několik paměťových míst. Tato místa typu paměti se nazývají registry. Takže v počítači mohou být skupiny bajtů dočasně uloženy v paměti nebo v registrech mikroprocesoru.
V kterémkoli z těchto úložišť může každá buňka mít buď 1, nebo 0 a nic jiného. V životě existují kladná a záporná čísla. Kladné číslo začíná znaménkem plus (+) a záporné číslo začíná záporným znaménkem (-). Pokud je znaménko vynecháno, je číslo považováno za kladné číslo.
Aby se vyřešil tento problém indikace znaménka čísla v počítači, jsou celá čísla uložena v rozsazích. Celá čísla jsou celá čísla. Pokud se k uložení rozsahu možných čísel použije osm bitů, použije se jako bit znaménka bit zcela vlevo. Pokud číslo začíná nulou, je to kladné číslo. Pokud začíná 1, je číslo záporné. Pokud se k uložení rozsahu možných čísel použije šestnáct bitů, použije se jako bit znaménka bit zcela vlevo. Pokud číslo začíná 0, t je číslo kladné číslo. Pokud začíná 1, je číslo záporné. Čísla v tomto tvaru se nazývají čísla se znaménkem.
V praxi mohou být čísla se znaménkem pro 8 bitů, 16 bitů, 32 bitů a 64 bitů. Čím širší je počet bitů, tím větší je rozsah možných čísel, která lze uložit.
Dvojka doplňte celá čísla
S dvojkovým doplňkem jsou kladná čísla normálními počítacími čísly, kromě toho, že číslice zcela vlevo je 0. Chcete-li získat odpovídající záporné číslo pro jakékoli dané kladné číslo, invertujte každý bit v čísle a k výsledku přidejte 1. Invert nebo doplněk 0 je 1. Invert nebo doplněk 1 je 0. Následující tabulky ukazují čísla dvou doplňku v jejich rozsazích:
| Tabulka 3.31 Dva doplňují celá čísla ve dvou bitech |
|
|---|---|
| Binární | Desetinný |
| 01 | +1 |
| 00 | +0 |
| jedenáct | -1 |
| 10 | -2 |
Kladná binární čísla jsou 00 a 01 (tedy nula a jedna). V bitu zcela vlevo nula ukazuje, že jde o kladná čísla. 00 je poněkud uprostřed rozsahu. Abychom získali -1, zjistíme, že inverze čísla 01 je 10. Přidáním 1 k tomuto (úplně vpravo) dostaneme 11.
Protože se používají dva bity, zbývá pouze jeden bit pro reprezentaci čísel v rozsahu, který se skládá z čísel +1, +0 a -1 odpovídajících 01, 00 a 11. První bit označuje znaménko. Stává se, že 10 pro +2 mezi těmito třemi binárními čísly není. 10 začíná 1, což znamená, že v doplňku dvojky musí být záporné číslo. Takže 10 je zahrnuto v rozsahu, což znamená -2.
Se dvěma bity ve dvojkovém doplňku je počet všech celých čísel (kladných a záporných), která lze reprezentovat, 2 2 = 4 a ne 2 2 -1 = 3. Nuance je výsledkem zahrnutí posledního záporného čísla, které je záporné číslo 2 číslos – 1. V tomto případě –2 2-1 = -2 1 = -2. V rozsahu čísel dvojkového doplňku ve 2 bitech není +2.
| Tabulka 3.32 Dva doplňují celá čísla ve čtyřech bitech |
|
|---|---|
| Binární | Desetinný |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Kladná binární čísla jsou od 0000 do 0111 (tedy od nuly do sedmi). V bitu zcela vlevo nula ukazuje, že jde o kladná čísla. 0000 je poněkud uprostřed rozsahu. Abychom získali -1, bylo zjištěno, že invert čísla 0001 je 1110. Přidáním 1 k tomuto (zcela vpravo) dostaneme 1111. Chcete-li získat -2, zjistíme, že invert 0010 je 1101. Přidáním 1 k tomuto ( z krajní pravice) dává 1110. Ostatní záporná binární čísla jako -3 až -7 jsou určena podobně.
Protože se používají čtyři bity, zbývají tři bity pro reprezentaci čísel v rozsahu, který je +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 a -7 odpovídající 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011 a 101.
-8, která odpovídá 1000, musí být adresována samostatně. První bit pro všechna tato čísla označuje znaménko 0 pro kladná čísla a 1 pro záporná čísla. Stává se, že 1000 není mezi těmito čtrnácti binárními čísly. 1000 začíná 1, což znamená, že musí být záporné číslo, pokud jde o dvojkový doplněk. Takže 1000 je zahrnuto v rozsahu, což znamená -8.
Se čtyřmi bity ve dvojkovém doplňku je počet všech celých čísel (kladných a záporných), která lze reprezentovat, 2 4 = 16 a ne 2 4 – 1 = 15. Nuance je výsledkem zahrnutí posledního záporného čísla, které je záporné číslo 2 čísloŠířka – 1. V tomto případě –2 4 -1 = -2 3 = -8. V rozsahu čísel není +8.
Předchozí analýzu pro dva, čtyři a širší bity ve dvojkovém doplňku lze aplikovat na binární čísla o šířce 8 bitů, 16 bitů, 32 bitů a 64 bitů.
Dvojkový doplněk obětuje první (zcela vlevo) bit pro znaménko 0 pro kladné číslo a 1 pro záporné číslo. Pro „n“ bitovou širokou skupinu bitů existují 2 n celkem kladná plus záporná čísla. Bylo by to 2 n -1, nebýt toho šťastného posledního (nejmenšího) záporného čísla. Nejvyšší kladné číslo je +2 n-1 -1 a nejmenší záporné číslo je -2 n-1 -1. Bylo by to -2 n-1 -1, nebýt toho šťastlivce -2 n-1 zahrnuta.
Odečítání čísel ve dvojkovém doplňku
Při odečítání:
A – B = D
A se nazývá minuend, B se nazývá subtrahend a D se nazývá rozdíl.
Pro odečtení jednoho kladného binárního čísla od jiného kladného binárního čísla se minuend zapíše do dvojkového doplňku a subtrahend se převede na jeho zápornou dvojkovou hodnotu. Matematické tvrzení tedy zní:
A+ – B = D
Jinými slovy, při odečítání dvojkového doplňku je subtrahend převeden na záporné číslo a poté přidán k minuendu.
Příklad 3.31:
Vyhodnoťte následující desítkový výraz ve dvou doplňcích pomocí čtyř bitů:
6 – 4
Řešení:
Binární číslo pro 6 je 110. Ve 4bitovém dvojkovém doplňku je to 0110. Binární číslo pro +4 je 100. Ve 4bitovém dvojkovém doplňku je to 0100. 0100, které musí být převedeno na zápornou 4 ve dvojce doplňte takto: Doplněk nebo inverze 0100 je 1011. Přidáním 1 z pravého konce, jak jsme to udělali navíc, dostaneme 1100. Desetinný výraz je tedy:
6 – 4, která se stává:
0110 – 0100, což je
0110 +(– 0100) = 0110 + 1100 provedeno jako v předchozí části přidání jako:

Poznámka: 0110 +(– 0100) je stejné jako 6 + – 4
Při odečtení dvojkového doplňku je jakékoli přenášení po posledním sloupci vlevo v sčítání zahozeno. Při odčítání v desítkové soustavě je matematický výrok:
6 – 4 = 2
Když uděláte totéž ve dvou doplňcích, odpověď je 0010, což je +2 v binárním počítání dvou doplňků. Předchozí odečítání odečte menší číslo od většího čísla. V následujícím příkladu je větší číslo odečteno od menšího čísla. V tabulce 3.32 lze zjistit, zda 0010 je skutečně dvojkový doplněk, který je ekvivalentní +2.
Příklad 3.32:
Vyhodnoťte následující desetinný výraz ve dvou doplňcích se čtyřmi bity:
4–6
Řešení:
Binární číslo pro 4 je 100. Ve 4bitovém dvojkovém doplňku je to 0100. Binární číslo pro +6 je 110. Ve 4bitovém dvojkovém doplňku je to 0110. 0110 musí být převedeno na zápornou 6 ve dvojkovém doplňku takto: Doplněk nebo inverze 0110 je 1001. Přidáním 1 k tomu z pravého konce, jak jsme to udělali v předchozím sčítání, dostaneme 1010. Desetinný výraz je tedy:
4-6, které se stávají:
0100 – 0110, což je
0100 +(– 0110) = 0100 + 1010 provedeno jako v předchozí části přidání jako:

Poznámka: 4+ – 6 je totéž jako 0100 +(– 0110).
Při odečtení dvojkového doplňku je jakékoli přenášení po posledním sloupci vlevo v sčítání zahozeno. Při odčítání v desítkové soustavě je matematický výrok:
4 – 6 = -2
Když uděláte totéž ve dvou doplňcích, odpověď je 1110, což je -2 v binárním počítání dvou doplňků. V tabulce 3.32 lze zjistit, zda 1110 je skutečně dvojkový doplněk, který je ekvivalentní pro -2.
3.4 Násobení binárních čísel
V prohlášení:
A x B = P
A se nazývá multiplikand, B se nazývá multiplikátor a P se nazývá součin. Výraz A x B znamená sečíst A, B kolikrát, když A a B jsou celá čísla (celá čísla).
Násobení v dvojkové soustavě je stejné jako násobení v desítkové soustavě. Místo v desítkové soustavě se to však provádí v binární podobě. Násobení desetinného výrazu 42 x 10 se provádí v binárním systému následovně, kde 42 10 = 101010 2 a 10 10 = 1010 2 :
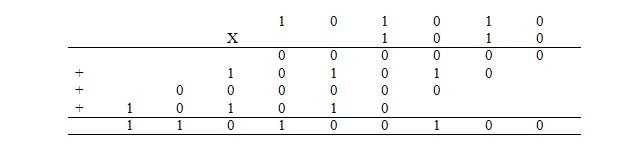
4 čísla, která se přidávají, se označují jako dílčí produkty. Odpovědí je produkt. Přidávání dílčích produktů se provádí stejným způsobem, jak bylo vysvětleno výše.
Násobení lze vidět také následovně: Při tomto násobení se dvěma základními hodnotami, je-li bit (číslice) v násobiteli 1, je nejméně významným bitem jeho dílčího součinu nejméně významný bit násobiče, který je přetypován přímo pod něj; a zbytek bitů multiplikandu se opakuje doleva. V tomto násobení se základem dva, pokud je bit (číslice) v násobiteli 0, jeho dílčí součin se skládá z nul s nejnižším významným bitem 0 přímo pod ním. Počet všech nul je počet bitů v multiplikandu.
3.5 Dělení binárních čísel
V prohlášení:
A ÷ B = Q
A se nazývá dividenda, B se nazývá dělitel a P se nazývá podíl. Kvocient může být doprovázen zbytkem. Výraz A ÷ B znamená, kolikrát může být B přidáno, aby vzniklo A nebo bylo blízko k němu tak, že zbytek je 0 nebo menší než B.
Rozdělení lze provést mnoha způsoby. Rozdělení, které je zde zobrazeno, je oddělení restaurování.
Obnovující divize
Toto je metoda dlouhého dělení, která se učí ve školách. Pokud je 237 děleno 6, odpověď je 39 zbytek 3. 237 10 v základu 2 je 11101101 2 a 6 10 v základu 2 je 110 2 . 39 10 v základu 2 je 100111 2 a 3 10 v základu 2 je 11 2 .
Takže 11101101 2 děleno 110 2 dává 100111 2 zbytek 11 2 v základu dva. S metodou obnovy jsou binární čísla běžná čísla a nemusí být nutně ve dvojkovém doplňku. Následující struktura rozděluje 11101101 2 do 110 2 dát 100111 2 zbytek 11 2 :

Odečítání se provádí běžně a ne pomocí doplňku dvou. Protože se jedná o základ dvě, výpůjčka je dvě a ne deset. Částečné dividendy jsou 10, 101, 1011, 1010 a 1001. 11 je zbytek. Protože je dělitel třímístný, dělení se provádí zásadně ve skupinách po třech číslicích z daného dělitele. Kvocient je celé číslo (celé číslo) a pro tento problém je to 100111. Výsledek podílu a zbytku je podle očekávání.
3.6 Aritmetické operace se softwarem a hardwarem
Základní deska počítače má hodiny. Tikání hodin se nazývá pulsy. Při každém taktu se na různých místech základní desky učiní jedno nebo více rozhodnutí; a to souvisí s programováním (softwarem).
Uvnitř mikroprocesoru jsou dva druhy obvodů nazývané: kombinované logické obvody a sekvenční logické obvody. Existuje další druh obvodu zvaný multiplexer. Sčítání, násobení a dělení může probíhat v rámci jednoho hodinového intervalu pomocí kombinační logiky (obvodu). Zatímco programování (software) provádí rozhodnutí při každém hodinovém impulsu pomocí sekvenčních logických obvodů a multiplexerů.
Když se odečítání provádí pomocí dvojkového doplňku, jsou nutné alespoň dva hodinové impulsy. Při prvním hodinovém impulsu multiplexor nasměruje subtrahend do sady hradel NOT (jedna brána NOT na číslici). Při druhém hodinovém impulsu kombinační logika přidá 1 k výstupu hradel NOT a pokračuje v přidávání výsledného subtrahendu a minuendu. Celé toto přidávání může proběhnout v rámci jednoho hodinového intervalu.
Sčítání, násobení a dělení může být stále nefunkční při programování pomocí pravdivostních tabulek. To však není zahrnuto v tomto online kariérním kurzu.
3.7 Logické operace v mikroprocesoru
AND, OR, XOR a Invert
A
Následující tabulka ilustruje bitový součin. To znamená, že pro dvě různá binární čísla jsou odpovídající bity spojeny AND na základě tabulky pravdy AND:
Pohyb zleva doprava, 1 AND 1 = 1; 0 AND 1 = 0; 0 A 0 = 0; 1 A 0 = 0; a tak dále v souladu s tabulkou pravdy AND.
NEBO
Následující tabulka ilustruje bitový OR. To znamená, že pro dvě různá binární čísla jsou odpovídající bity OR na základě tabulky OR pravdy:

Pohyb zleva doprava, 1 NEBO 1 = 1; 0 NEBO 1 = 1; 0 NEBO 0 = 0; 1 NEBO = 1; a tak dále v souladu s tabulkou pravdy OR.
VOLNÝ, UVOLNIT
Následující tabulka ilustruje Bitwise exclusive-OR. To znamená, že pro dvě různá binární čísla jsou odpovídající bity XORed na základě tabulky pravdy XOR:

Pohyb zleva doprava, 1 XOR 1 = 0; 0 XORi = 1; 0 XOR 0 = 0; 1 XOR° = 1; a tak dále v souladu s XOR Truth Table.
Invertovat (NE)
Následující tabulka ilustruje Bitwise NOT (invertovat). To znamená, že pro jedno binární číslo je tentokrát každý bit invertován na základě NOT Truth Table:

Pohyb zleva doprava, NE 1 = 0; NE 0 = 1; NE 0 = 1; NE 1 = 0; a tak dále v souladu s tabulkou NOT Truth Table.
Řazení doprava nebo doleva
Shift vpravo
Následující binární číslo je posunuto o 3 bitové pozice doprava, s nulami vloženými do uvolněných bitových pozic vlevo:

Řazení lze provést o jedno, dvě, tři, čtyři atd. místa.
Shift doleva
Následující binární číslo je posunuto o 3 bitové pozice doleva, s nulami vloženými do uvolněných bitových pozic vpravo:

Řazení lze provést o jedno, dvě, tři, čtyři atd. místa.
Otáčení doprava nebo doleva
Otáčení je podobné řazení. Dělá se to jeden kousek po druhém. Při otáčení doprava bity, které opouštějí pravý konec, nepadají jako při řazení; nahrazují uvolněné bity vlevo, jeden po druhém. Při otáčení doleva bity, které opouštějí levý konec, nepadají jako při řazení; nahrazují uvolněné bity vpravo, jeden po druhém.
Otočit doprava
Následující binární číslo je otočeno o 3 bitové pozice doprava:

Otáčení lze provést o jedno, dvě, tři, čtyři atd. místa.
Rorate vlevo
Následující binární číslo je otočeno o 3 bitové pozice doleva:

Otáčení lze provést o jedno, dvě, tři, čtyři atd. místa.
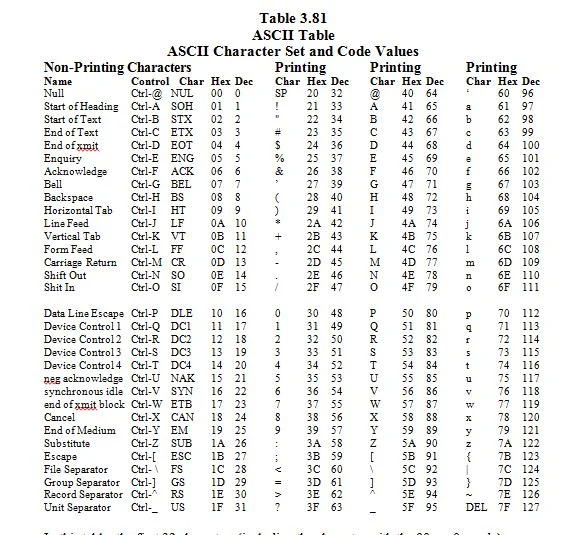
3.8 Znaková sada ASCII a její kódové hodnoty
ASCII je zkratka pro „American (U.S.A) Standard Code for Information Interchange“. Představte si klávesnici s 96 klávesami. Toto je ideální klávesnice, kde se klávesy s velkými písmeny liší od kláves s malými písmeny. Každá druhá klávesa představuje znak, který se nachází na anglické (U.S.A) klávesnici. Znaky a kódy (odpovídající čísla znakům) jsou uvedeny v následujícím seznamu:
V této tabulce je prvních 32 znaků (včetně znaku s 00 16 = 0 10 kód) jsou netisknutelné znaky. Jsou to řídící postavy. Nejsou vidět na obrazovce (monitoru), kde je vše stejné. Mají pouze účinky. Promluvme si o tom později.
Zbytek znaků jsou tiskací znaky; jsou vidět na obrazovce. Obsahuje 128 znaků ASCII. 2 7 = 128,1111111 2 = 127 10 . 7 ve 2 7 znamená 7 bitů.
Nyní, 1111111 2 + 1 2 je stejné jako:
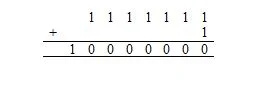
Tady 10 000 000 2 = 128 10 . Je jich 128 10 znaky v předchozím seznamu (tabulce) znaků ASCII. To zahrnuje znak null, jehož kód v šestnáctkovém (hexadecimálním) základu je 00, což je ekvivalentní 0 v základu deset.
Protože je celkem 128 znaků, 128 mínus 32 netisknutelných znaků dává 96 tiskových znaků. V této části se předpokládá, že existuje ideální klávesnice s 96 znaky, které jsou tisknutelné znaky. Na této ideální klávesnici se klávesy velkých anglických znaků liší od kláves malých anglických znaků.
Každý znak na klávesnici je reprezentován základním počtem 7 bitů, které nejsou uvedeny v seznamu. Například velké písmeno „N“ je reprezentováno sedmi bity 1001110 v základu 2. Chcete-li převést 1001110 2 na základ 16, před ní 0 a seskupte výsledek do čtyřbitových podskupin takto:
| 0100 | 1110 | 2 = | 4 | E | 16
To je 01001110 2 = 4E 16 . Chcete-li převést 4E 16 pro základ deset proveďte následující:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
Napravo od „N“ v seznamu (tabulce) je šestnáctkové číslo 4E a desítkové číslo 78.
Jako další příklad je znak „[“ reprezentován sedmi bity 1011011 v základu 2. Chcete-li převést 1011011 2 na základ 16, před ní 0 a seskupte výsledek do čtyřbitových podskupin takto:
| 0101 | 1011 | 2 = | 5 | B | 16
To je 01011011 2 = 5B 16 . Chcete-li převést 5B16 na základ deset, postupujte takto:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
Napravo od „[“ v seznamu (tabulce) je šestnáctkové číslo 5B a desítkové číslo 91.
Jako další příklad je znak pro desetinné číslo „5“ reprezentován sedmi bity 0110101 v základu 2 a ne 0000101 v základu 2. Chcete-li převést 0110101 2 na základ 16, před ní 0 a seskupte výsledek do čtyřbitových podskupin takto:
| 0011 | 0101 | 2 = | 5 | B | 16
To je 00110101 2 = 35 16 . Chcete-li převést 3516 na základ deset, postupujte takto:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
Napravo od „5“ v seznamu (tabulce) je šestnáctkové číslo 35 a desetinné číslo 53.
Vzhledem k tomu, že počítač pracuje v bytech, při stisku klávesy na ideální klávesnici se do mikroprocesoru (základní desky) odešle osm bitů. Ideální klávesnice je periferie, která je oddělena od systémové (základní) jednotky počítače. Má elektronický obvod (IC), který vytváří sedm bitů a předchází mu nulu, než jej pošle kabelem na základní desku systémové jednotky. Ze vstupního portu (vstupního obvodu) základní desky jde do mikroprocesoru, který je také na základní desce. Z mikroprocesoru jde do paměti, která je také osazena na základní desce.
Takže po stisknutí klávesy „N“ na ideální klávesnici se do mikroprocesoru přenese osm bitů 01001110. Z mikroprocesoru jsou přeneseny do paměti, kde zůstávají v paměťovém místě jako byte. Počítačový programátor by měl mít na paměti, že osm bitů 01001110 2 je stejný jako 4E 16 což je stejné jako 78 10 .
Po stisknutí klávesy „[“ na ideální klávesnici se do mikroprocesoru přenese osm bitů 01011011. Z mikroprocesoru jsou přeneseny do paměti, kde zůstávají v paměťovém místě jako byte. Počítačový programátor by měl mít na paměti, že osm bitů 01011011 2 je stejný jako 5B 16 což je stejné jako 91 10 .
Po stisku klávesy „5“ na ideální klávesnici se jako znak a nikoli jako desetinné číslo přenese do mikroprocesoru osm bitů 00110101. Z mikroprocesoru jsou přeneseny do paměti, kde zůstávají v paměťovém místě jako byte. Počítačový programátor by měl mít na paměti, že osm bitů 00110101 2 je stejný jako 35 16 což je stejné jako 5310 10 .
Jsou chvíle, kdy program běží a čeká na vložení desetinného čísla 5 do počítače. V této situaci, pokud je stisknuta klávesa „5“ na ideální klávesnici, stále se do mikroprocesoru přenese osmibitový kód 00110101. Protože je potřeba desetinné číslo 5, a nikoli znak „5“, část kódu (krátký program) z paměti používá mikroprocesor k převodu znakového kódu 00110101 v základu dvě na číslo doplňku dvojky 00000101. 2 před odesláním do paměťového místa jako bajt doplňku dvojky. Počítačový programátor musí mít na paměti, že 00000101 znamená 5 10 v základu 2 a liší se od kódových čísel 00110101 2 , 35 16 a 53 10 což znamená znak „5“. Aby bylo možné v paměti zobrazit dvojkové číslo doplňku 00000101, musí jiný krátký program převést 00000101 z paměti na 00110101. Je to 00110101, což je stejné jako 35 16 což je stejné jako 53 10 který je zobrazen na monitoru (nebo vytištěn na papíře tiskárnou).
3.9 Formát čísel s pohyblivou řádovou čárkou
Číslo bez desetinné části je celé číslo. Číslo 36 je celé číslo. 36,375 není celé číslo. Je to desetinné číslo s desetinnou částí. Desetinná část 0,375 je zlomek, který je menší než 1.
36.375 se interpretuje v desítkové podobě jako:
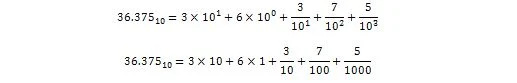
Nyní:
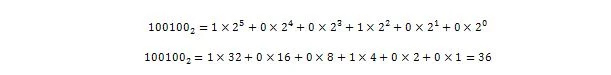
Takže 100 100 2 = 3610, což je celá číselná část 36,375 10 .
Nyní:
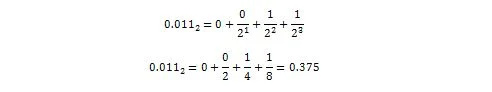
Takže 0,011 2 = 0,375 10 což je část desetinného čísla 36,375 10 .
∴ 36,375 10 = 100100,011 2
Řekni to jinak:
100100,011 2 = 36,375 10
Čísla jsou v počítači zastoupena v základu 2 a ne v základu 10, přičemž vše je stejné. Protože buňka v registru v mikroprocesoru nebo buňka v paměti může mít pouze 1 nebo 0, není zde místo pro uložení desetinné čárky. To představuje problém. Jako rozlišení je k dispozici IEEE-754 jednoduchá 32bitová reprezentace s plovoucí desetinnou čárkou a IEEE-754 dvojitá přesnost 64bitová reprezentace s plovoucí desetinnou čárkou.
32bitový formát čísel s pohyblivou řádovou čárkou
Číslo 100100.0112 lze vyjádřit jako:
100100,011 2 = 1,00100011 2 x 2 +5
Pravá strana symbolu = je v matematice označována jako základní dvě standardní formy levé strany 100100.011 2 .
Nyní 00100011 z 1,00100011 2 na pravé straně symbolu = bez předchozího „1“. a bez 2 pro základ se nazývá explicitní significand. V tomto případě je binární bod umístěn o pět míst vlevo, aby měl „1“. Nezaměňujte mezi desetinnou čárkou a binární čárkou. Binární tečka je pro základ 2, zatímco desetinná čárka je pro základ 10. „1“. následovaný 00100011 na pravé straně symbolu =, bez 2 pro základ, tvoří skutečný significand. Nicméně 1,00100011 se nazývá implicitní significand.
Po significand na pravé straně je „x 2 +5 “výraz. S tímto výrazem se +5 nazývá exponent. Znaménko plus znamená, že binární bod se musí posunout o pět míst dopředu, aby byl na své normální původní pozici, a 2 je základ pro číslování. Předchozí rovnici lze zapsat obráceně jako:
1,00100011 2 x 2 +5 = 100100,011 2
Při 32bitové reprezentaci s pohyblivou řádovou čárkou je to „1,00100011 2 x 2 +5 “, který se používá a nikoli pouze „100100.011 2 “. 2 pro základ se nezaznamenává. 32bitová reprezentace s pohyblivou řádovou čárkou pro „1.00100011 2 x 2 +5 ” číslo, které se rovná 36,375 10 = 100100,011 2 , je zobrazen v následující tabulce:

Existují 32bitové pozice, které jsou číslovány od pravého konce, počínaje 0. První bit na levém konci je znaménkový bit. Pokud je číslo kladné, je tento bit 0. Je-li číslo záporné, je tento bit 1 (-1 se skládá ze dvou znaků a nelze je vložit do žádné buňky). 1,00100011 2 x 2 +5 což se rovná 36,375 10 což se také rovná 100100,011 2 je kladné číslo. Takže první bit je 0.
Exponent má osm bitových pozic, počínaje od pozice 30 do pozice 23 včetně. Exponent, který je tam zapsán, je však 10000100 2 což se rovná 132 10 . Exponent počtu úroků je ve skutečnosti +5 ze základu dvou. Takže, co se stane?
Nyní ve 32bitovém formátu je exponent 0 zapsán jako 01111111 2 což se rovná 127 10 . +5 10 je +101 2 . Takže při příchodu na 1 000 100 2 v exponentní části v tabulce, 101 2 byl přidán k 01111111 2 , odpovídajícím způsobem. To znamená, že 5 bylo přidáno ke 127, aby bylo 132 10 .
Significand bez „1.“ obsadil pozice 22 až 15 včetně. Všimněte si, že 1 z „1“. nebyla uvedena v 32bitovém řetězci. Nikdy to není naznačeno – přijměte to. Zbytek buněk až do pozice 0 je vyplněn nulami.
Pokud je skutečný exponent -5, pak se 5 odečte od 127 10 mít 122 10 . To odpovídá odečtení 101 2 od 01111111 2 mít 01111010 2 .
U všech předchozích ilustrací číslo +1, které se rovná 1,0 x 2 0 = 1,0 x 1 = 1,0 je reprezentováno jako:

Všimněte si, že '1.' 1,0 x 2 0 není uvedeno ve formátu. Nikdy to není indikováno. Další smíšený zlomek, který je po 1,0 kladný, je:

Všimněte si 1 na pravém konci. Tato reprezentace je číslo:

Rozdíl mezi 1,0000001192092896 a 1,0 je:
1,0000001192092896 – 1,0 = 0,0000001192092896
Čísla s desetinnými částmi jsou smíšené zlomky. Ne všechny zlomky mezi 1 10 a 2 10 mohou být zastoupeny v počítači. Lze předpokládat, že nejmenší zlomková mezera mezi po sobě jdoucími smíšenými čísly s 32bitovým formátem s plovoucí desetinnou čárkou je 0,0000001192092896. Očekávejte, že interval pro dvojnásobnou přesnost bude menší. Viz následující obrázek.
0,0 reprezentující číslo nenásleduje předchozí argumenty. Reprezentace pro 0,0 je deklarována a musí se jako taková naučit. Pro vyjádření 0,0 jsou všechny buňky pro significand 0 a všechny buňky pro exponent jsou také nula. Znaménkový bit může být 0 nebo 1. Bohužel to vede ke kladné 0 a záporné 0 následovně:

V reálném životě je jen jedna nula. Kladná 0 a záporná 0 neexistují. Nicméně 0 je obvykle považována za kladnou. Kladná 0 a záporná 0 zde existují kvůli tomuto konkrétnímu popisu formátu. Číselná řada (viz výše) může mít také +0 a -0, ale existuje pouze jedna nula.
64bitový formát čísel s plovoucí desetinnou čárkou
64bitový formát s plovoucí desetinnou čárkou je podobný 32bitovému formátu, ale s následujícími rozdíly:
- Číslo má 64 bitů.
- Po bitu znaménka následuje 11 bitů pro číslo exponentu.
- Číslo exponentu pro nulový index (2 0 ) je 1023 10 = 01111111111 2 .
- Po jedenácti bitech následuje 52 bitů pro explicitní significand.
- Má širší rozsah čísel než 32bitový formát.
Všimněte si, že '1.' který je na začátku significand stále není zahrnut mezi 64 bitů, stejně jako není zahrnut mezi 32 bity pro 32bitový formát.
Jedním z nejdůležitějších rozdílů mezi 64bitovým formátem a 32bitovým formátem je, že rozdíl mezi po sobě jdoucími smíšenými zlomky v 64bitovém formátu je menší než u 32bitového formátu.
V 64bitovém formátu lze interval (mezera) mezi 1,0 a dalším smíšeným zlomkem vypočítat následovně:
1.0 je
0 01111111111 00000000000000000000 00000000000 0000000000000000000000 2
To je ekvivalentní „1.“, které nebylo uvedeno v řetězci, vynásobené 2 umocněnou (index) 0 (s exponentem 1023 10 = 01111111111 2 za 2 0 = 1). Řetězec je 1,0 x 2 0 .
Další smíšený zlomek větší než 1,0 je:
0 01111111111 00000000000000000000 00000000000 0000000000000000000001 2
To je ekvivalentní „1“. který není uveden v řetězci, následuje 51 nul a pak 1, násobená 2 umocněnou na 0 (s exponentem 1023 10 = 011111111112 2 za 2 0 = 1). Toto je stejné jako:
+2 0 × (1 + 2- -52 ) ≈ 1,0000000000000002
≈ znamená přibližně rovno.
Nyní:
1,0000000000000002 – 1,0 ≈ 0,0000000000000002
Odpovídající hodnota intervalu pro 32bitový formát je 0,0000001192092896 ≈ 0,00000012.
0,000000000000002 je mnohem menší než 0,00000012. Mezi dvěma po sobě jdoucími celými čísly (např. 3 a 4) v 64bitovém formátu je tedy mnohem více smíšených zlomků než mezi dvěma po sobě jdoucími celými čísly pro 32bitový formát.
Počet smíšených zlomků mezi dvěma po sobě jdoucími celými čísly na číselné ose je nekonečný. Žádný formát (např. 32bitový nebo 64bitový) tedy nemůže poskytnout všechny smíšené zlomky mezi libovolnými dvěma po sobě jdoucími celými čísly (celými čísly). Čím menší je mezera (interval) mezi dvěma po sobě jdoucími celými čísly poskytovanými formátem (např. 32bitový nebo 64bitový), tím větší je počet smíšených zlomků mezi po sobě jdoucími celými čísly (pro číselnou řadu).
Důvody, proč je 64bitový formát popisován jako dvojnásobná nebo vyšší přesnost ve srovnání s 32bitovým formátem, jsou ten, že interval mezi dvěma po sobě jdoucími smíšenými zlomky ohraničenými dvěma po sobě jdoucími celými čísly pro 64bitový formát je menší než odpovídajících 32 -bitový formátový interval. Také existuje více možných smíšených zlomků mezi dvěma ohraničenými celými čísly pro 64bitový formát než odpovídajícím způsobem pro 32bitový formát.
Převod desetinné části (zlomku) desetinného čísla na binární část
36.375 je dekadické číslo s desetinnou částí „.375“. Desetinná část „.375“ je zlomek mezi nulou a jedničkou. 0,5 v základní desítce má stejnou hodnotu jako 1/2 v základní dva. 0,5 10 to je vyjádřeno rozšířením základu dva:
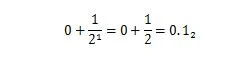
Není to 0,101 2 což znamená 0,625 10 . Desetinná část dekadického čísla má ekvivalentní binární část pro odpovídající binární číslo. Chcete-li tedy převést desetinné číslo, jako je 36,375 10 na základ dvě, převeďte 36 na binární a poté převeďte 0,375 také na binární. Poté oba výsledky spojte s binárním bodem. Metody převodu těchto dvou částí se liší. Jak převést dekadické celé číslo na základ 2 je vysvětleno v kapitole 1.
Chcete-li převést desetinný zlomek na binární zlomek, postupujte takto:
- Vynásobte desetinný zlomek (desetinnou část) 2. Celé číslo, které z toho vyplývá, je první binární číslice.
- Opakujte předchozí krok s výsledkem ve zlomcích desetinných míst, abyste získali další binární číslici.
- Opakujte předchozí krok, dokud nebude desetinný zlomkový výsledek 0,0000—.
Příklad: Převeďte zlomkovou část 36,375 10 na ekvivalentní zlomkovou část v základu dva.
Řešení:
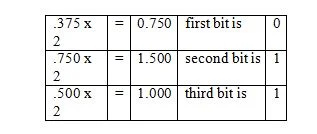
Všimněte si, že ve třetím kroku bylo 0,500 vynásobeno 2 a ne 1,500. Binární odpovídající zlomek se čte v posledním sloupci shora. A tak je výsledek následující:
.375 10 = 0,011 2
Převod binární části (zlomku) binárního čísla na desetinnou část
Chcete-li toho dosáhnout, rozšiřte binární zlomek na převrácené mocniny 2.
Příklad: Převeďte zlomkovou část 100100,011 2 na ekvivalentní zlomkovou část v základu deset.
Řešení:
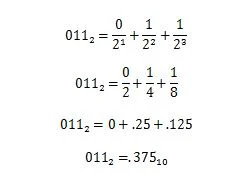
3.10 Předpony čísel ve výpočetní technice
V normálním životě 1 kilo znamená 1000, což je zkráceno v k (malá písmena) jako 1 kg. Ve výpočetní technice 1 kilo znamená 2 10 = 1024, ale je zkráceno v K (velká písmena) jako v 1 kB. V normálním životě 1 mega znamená 1 000 000, což je zkráceno v M (velká písmena) jako 1Mg. Ve výpočetní technice 1 mega znamená 2 dvacet = 1 048 576 = 2 10 x 2 10 = 1024 x 1024 = 1 048 576 a je stále zkráceno v M (velká písmena) jako v 1Mbit. V normálním životě 1 giga znamená, že 1 000 000 000 je zkráceno v G (velká písmena) jako v 1Gg. Ve výpočetní technice 1 giga znamená 2 30 = 1 073 741 824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1 073 741 824 a je stále zkráceno v G (velká písmena) jako v 1Gbitech. Následující tabulka uvádí význam čtyř prefixů v normálním životě a ve výpočetní technice:
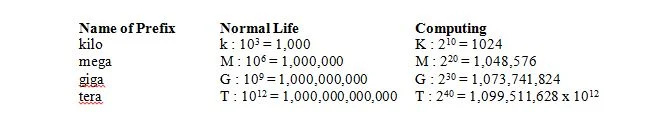
3.11 Problémy
Čtenáři se doporučuje vyřešit všechny problémy v kapitole, než přejde k další kapitole.
- Nakreslete číselnou osu s celými čísly od -10 do +10.
- Přidejte následující binární čísla v 8bitovém dvojkovém doplňku: 101010 2 a 1111 2 .
- K odečtení binárního čísla 1111 použijte pouze přístup dvojkového doplňku v 8 bitech 2 z binárního čísla 101010 2 .
- Najděte produkt 10110 2 x 1101 2 v základu dva.
- Dělit 36,375 10 o 1000 10 v desítkové a binární soustavě a porovnejte výsledky.
- Použijte 8 bitů podle svého výběru k ilustraci logického AND, OR, XOR, Invert, Shift Right, Shift Left, Rotate Right a Rotate Left. Každý bajt by měl obsahovat kombinaci 1 a 0.
- a) Napište číselný kód pro znak ASCII nula v šestnáctkové, binární a desítkové soustavě.
b) Napište číselný kód pro znak ASCII „1“ v šestnáctkové, binární a desítkové soustavě.
c) Napište číselný kód pro ASCII znak „A“ v šestnáctkové, binární a desítkové soustavě.
d) Napište číselný kód pro ASCII znak „a“ v šestnáctkové, binární a desítkové soustavě. - Převést 49,49 10 do základny dvě. Převeďte výsledek do 32bitového formátu IEEE s plovoucí desetinnou čárkou.
- a) Jak se liší 64bitový formát IEEE s pohyblivou řádovou čárkou od 32bitového formátu?
b) Uveďte dva související důvody, proč je 64bitový formát popsán jako dvojnásobná nebo vyšší přesnost oproti formátu
32bitový formát.